2  Výpočet velikosti měřené veličiny

2.1

Napětí s průběhem podle obrázku se měří: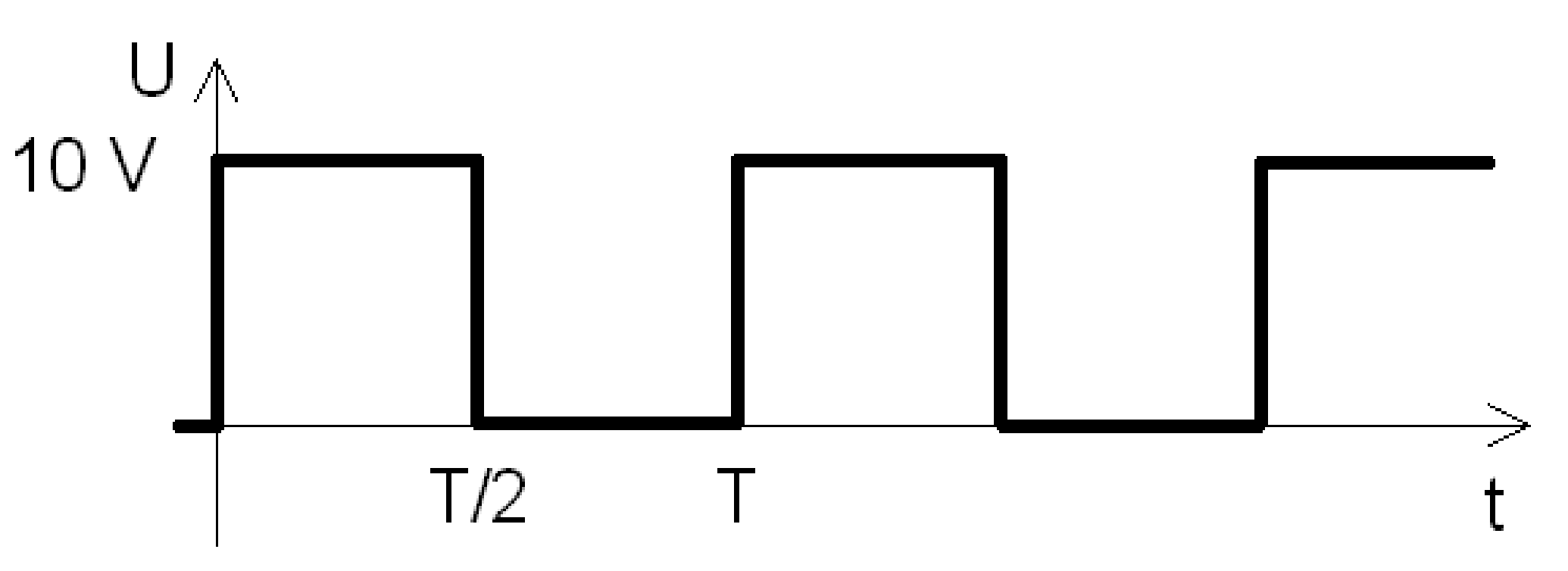

  1. číslicovým voltmetrem s operačním usměrňovačem bez oddělovací kapacity na vstupu [5,55 V]

  2. číslicovým voltmetrem s operačním usměrňovačem s oddělovací kapacitou na vstupu [5,55 V]

  3. číslicovým voltmetrem s převodníkem pro měření skutečné efektivní hodnoty (true RMS) [7,07 V]

Určete údaje jednotlivých přístrojů, mají-li všechny přístroje odpovídající rozsahy.

Číslivový voltmetr (bez funkce trueRMS) s operačním usměrňovačem bez oddělovacího kondenzátoru měří usměrněnou střední hodnotu a násobý naměřený údaj činitelem tvaru pro sinusový průběh (\(k = 1,11\)).

\[\begin{equation} \begin{split} U_{SU} & = \frac{1}{T} \int_0^T |u(t)| dt \\ & = \frac{1}{T} \int_0^{T/2} 10 dt \\ & = \frac{1}{T} [10t]_0^{T/2} \\ & = \frac{1}{T} \cdot 10 \frac{T}{2} = 5 V \end{split} \end{equation}\]

Nakonec opět vynásobíme koeficientem tvaru \(k = 1,11\) pro sinus, který používají pro přepočet levné multimetry.

Naměřená hodnota číslicovým voltmetrem s operačním usměrňovačem bez oddělovací kapacity na vstupu bude \(U = 5,55\,V\).

Pokud měříme signál číslicovým voltmetrem s operačním usměrňovačem s oddělovací kapacitou na vstupu, pak na signálu nebudeme pozorovat stejnosměrnou (DC) složku. Ta je oddělovacím kondenzátorem potlačena. Průběh za oddělovacím kondenzátorem je znázorněn na grafu níže. Usměrněná složka je poté znázorněna červenou šrafovanou čárou.

Code 
import matplotlib.pyplot as plt
import numpy as np

# Parametry signálu
T = 1  # perioda
t = np.linspace(0, 2*T, 1000)  # 2 periody
amplitude = 10
duty_cycle = 0.5

# Signál s kondenzátorem
signal_c = np.where((t % T) < duty_cycle * T, duty_cycle * amplitude, -(1 - duty_cycle) * amplitude)

# Usměrněný signál s kondenzátorem
rectified_signal = np.abs(signal_c)

# Vytvoření grafu
plt.figure(figsize=(5, 3))
plt.plot(t, signal_c, 'k-', linewidth=3)
plt.xlabel('Čas')
plt.ylabel('Napětí [V]')
plt.title('Signál za oddělovacím kondenzátorem')
plt.grid(True, alpha=0.3)
plt.xlim(0, 2)
plt.ylim(-6, 6)
plt.xticks([1, 2], ['T', '2T'])
plt.yticks(np.arange(-5, 6, step=5))

plt.plot(t, rectified_signal, 'r--', linewidth=2)

plt.tight_layout()
plt.show()

Nejprve spočteme stejnosměrnou složku: \[\begin{equation} \begin{split} U_{DC} & = \frac{1}{T} \int_0^T u(t) dt \\ & = \frac{1}{T} \cdot \left( \int_0^\frac{T}{2} 10 dt + \int_\frac{T}{2}^T 0 dt \right) \\ & = \frac{1}{T} \left( \frac{10T}{2} + 0 \right) \\ & = \frac{10}{2} = 5\, V \end{split} \end{equation}\]

Je vidět, že hodnota odpovídá grafu výše, kdy byla potlačena stejnosměrná (DC) složka a proto se signál posunul z obdélníkového unipolárního signálu (0V, 10V) na signál (-5V, 5V).

Vypočteme střední usměrněnou hodnotu napětí:

\[\begin{equation} \begin{split} U_{SU} & = \frac{1}{T} \int_0^T |u(t)| dt \\ & = \frac{1}{T} \int_0^{T} 5 dt \\ & = \frac{1}{T} [5t]_0^{T} \\ & = \frac{1}{T} \cdot 5T = 5 V \end{split} \end{equation}\]

Nesmíme zapomenout výsledek vynásobit činitelem tvaru \(k = 1,11\).

Naměřená hodnota číslicovým voltmetrem s operačním usměrňovačem s oddělovací kapacitou na vstupu bude \(U = 5,55\,V\).

Číslicový multimetr z funkcí TrueRMS bude ukazovat efektivní hodnotu odpovídající přímo definici efektivní hodnoty pro daný signál.

\[\begin{equation} \begin{split} U & = \sqrt{\frac{1}{T} \int_0^T u^2(t) dt} \\ & = \sqrt{\frac{1}{T} \int_0^\frac{T}{2} 10^2 dt} \\ & = \sqrt{50} = 7,07 V \end{split} \end{equation}\]

Naměřená hodnota číslicovým voltmetrem s převodníkem pro měření skutečné efektivní hodnoty (true RMS) bude \(U = 7,07\,V\).

2.2

Napětí s průběhem podle obrázku se měří: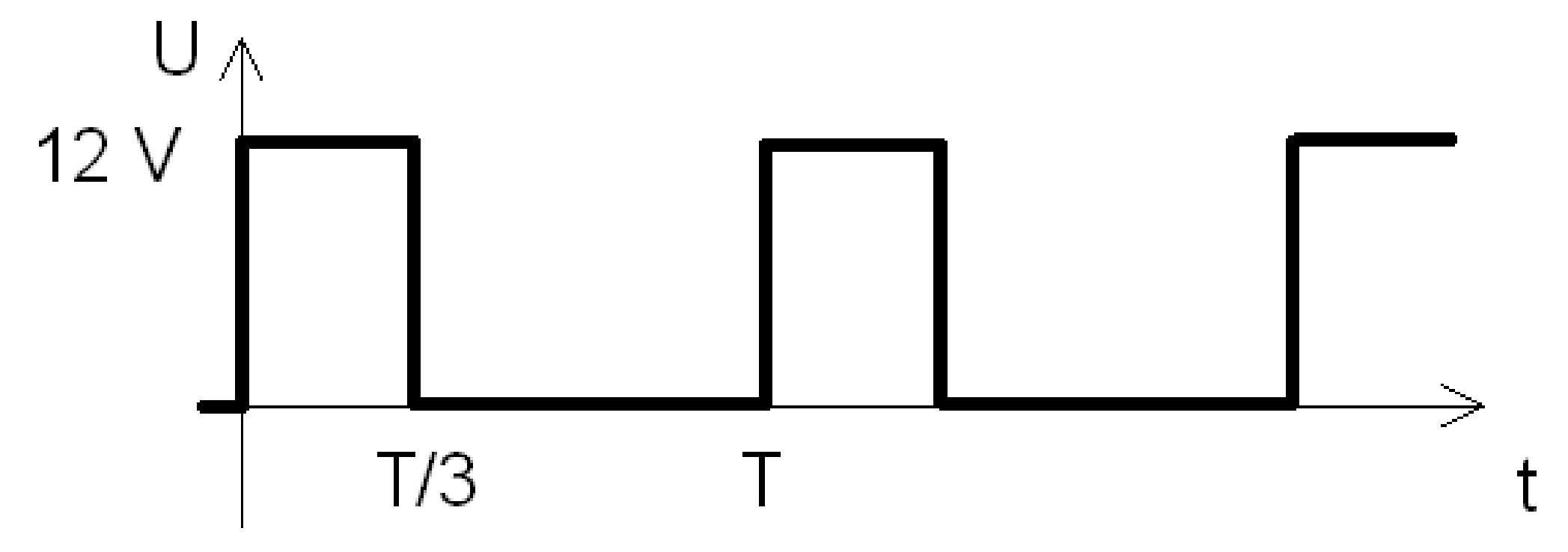

  1. číslicovým voltmetrem s operačním usměrňovačem bez oddělovací kapacity na vstupu [4,44 V]

  2. číslicovým voltmetrem s operačním usměrňovačem s oddělovací kapacitou na vstupu [5,92 V]

  3. číslicovým voltmetrem s převodníkem pro měření skutečné efektivní hodnoty (true RMS) [6,93 V]

Určete údaje jednotlivých přístrojů, mají-li všechny přístroje odpovídající rozsahy.

2.3 Interaktivní příklad

Code 
viewof amplitude = Inputs.range([0.5, 15], {value: 10, step: 0.1, label: "Amplituda [V]:"})
viewof dutyCycle = Inputs.range([0, 1], {value: 0.5, step: 0.05, label: "Střída:"})

// Plot waveform
Plot.plot({
  title: "",
  width: 600,
  height: 200,
  x: {label: "Čas", domain: [0, 2], ticks: [0, 1, 2], tickFormat: (d) => d === 0 ? "0" : d === 1 ? "T" : "2T"},
  y: {label: "Napětí [V]", domain: [0, amplitude * 1.1]},
  marks: [
    Plot.line(
      Array.from({length: 1000}, (_, i) => {
        const t = (i / 1000) * 2; // 2 periods
        const phase = (t % 1); // normalize to 1 = one period
        return {
          x: t,
          y: phase < dutyCycle ? amplitude : 0
        };
      }),
      {x: "x", y: "y", stroke: "black", strokeWidth: 4}
    ),
    Plot.ruleY([0]),
    Plot.ruleX([1], {stroke: "gray", strokeDasharray: "2,2"}) // mark the end of first period
  ]
})
Code 
mean_dc = amplitude * dutyCycle
average = mean_dc * 1.11 // simulation of meter scaling factor

/*
  ⚠️ Note for students:
  The formulas apply only to a unipolar rectangular waveform (0 ↔ U).
  They are derived directly from the basic definitions of
  mean value, rectified mean value, and RMS value.
*/

// b) Mean value with coupling capacitor (rectified AC component)
mean_ac_rec = 2 * amplitude * dutyCycle * (1 - dutyCycle)
rectified_avg_ac = mean_ac_rec * 1.11 // simulation of meter scaling factor

// c) True RMS value
rms = amplitude * Math.sqrt(dutyCycle)

// Display results
html`
<p>a) číslicovým voltmetrem s operačním usměrňovačem bez oddělovací kapacity na vstupu: ${average.toFixed(2)} V</p>
<p>b) číslicovým voltmetrem s operačním usměrňovačem s oddělovací kapacitou na vstupu: ${rectified_avg_ac.toFixed(2)} V</p>
<p>c) číslicovým voltmetrem s převodníkem pro měření skutečné efektivní hodnoty (true RMS): ${rms.toFixed(2)} V</p>
`